A new algorithm of evaluation of Wigner Distribution Function with application to radio occultation analysis
Michael
Gorbunov
A.M. Obukhov Institute of Atmospheric Physics, Russian Academy of Sciences
Poster
Time-frequency representation is a powerful technique for the analysis of radio occultation (RO) data. It includes sliding-spectrum analysis, or spectrogram, Wigner Distribution Function (WDF), Kirkwood Distribution Function (KDF), and their modifications based on the reassignment technique. Using these techniques, a signal as a 1-D function of time is mapped to 2-D phase or ray space, where each point can be associated with a geometric optical ray. This space is parameterized by coordinate and momentum. Two possible parameterizations: (time – Doppler frequency) and (impact parameter – bending angle) are linked to each other by a canonical transform. WDF demonstrates a higher resolution as compared to spectrogram and more regular behavior as compared to KDF. On the other hand, the evaluation of WDF requires high computational costs, while the evaluation of KDF is fast.
In this study, we apply the theory of WDF, KDF, and Fourier integral operators (FIOs) to develop a fast algorithm of the evaluation of WDF. We employ the fact that between WDF and KDF there are forward and inverse convolution relations. We consider the rotation group of the phase space. This group consists of canonical transforms, which are implemented as FIOs describing the dynamics of the harmonic oscillator. Such FIOs form the group of fractional Fourier transforms. The fundamental property of WDF is its invariance with respect to canonical transforms. KDF does not possess this property. However, we consider KDF averaged over the rotation group. Because KDF equals WDF convolved with the corresponding kernel, its straightforward to arrive at the expression of the KDF averaged over the rotation group. WDF is invariant, and, therefore, the averaged KDF equals WDF convolved with the averaged convolution kernel. The latter is explicitly expressed through Bessel function. Finally, this procedure results in WDF smoothed over a quantum cell in the phase space.
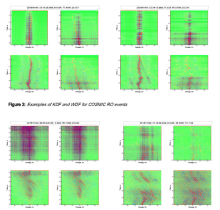
We implemented the algorithm numerically. The fractional Fourier transform can be represented as a composition of multipliers and Fourier transforms, which means that it allows a fast numerical implementation. We perform averaging over a finite number of rotation angles, which allows the performance optimization. We give examples of processing artificial and real RO events.
This work was supported by Russian Foundation for Basic Research (grant No 20-05-00189 A).
In this study, we apply the theory of WDF, KDF, and Fourier integral operators (FIOs) to develop a fast algorithm of the evaluation of WDF. We employ the fact that between WDF and KDF there are forward and inverse convolution relations. We consider the rotation group of the phase space. This group consists of canonical transforms, which are implemented as FIOs describing the dynamics of the harmonic oscillator. Such FIOs form the group of fractional Fourier transforms. The fundamental property of WDF is its invariance with respect to canonical transforms. KDF does not possess this property. However, we consider KDF averaged over the rotation group. Because KDF equals WDF convolved with the corresponding kernel, its straightforward to arrive at the expression of the KDF averaged over the rotation group. WDF is invariant, and, therefore, the averaged KDF equals WDF convolved with the averaged convolution kernel. The latter is explicitly expressed through Bessel function. Finally, this procedure results in WDF smoothed over a quantum cell in the phase space.
We implemented the algorithm numerically. The fractional Fourier transform can be represented as a composition of multipliers and Fourier transforms, which means that it allows a fast numerical implementation. We perform averaging over a finite number of rotation angles, which allows the performance optimization. We give examples of processing artificial and real RO events.
This work was supported by Russian Foundation for Basic Research (grant No 20-05-00189 A).
Poster PDF